What is a triangle?

A triangle is a 2D shape with 333 straight sides and 333 vertices. You need to be able to classify triangles based on their properties, and find unknown angles and side lengths. 

What is a triangle?

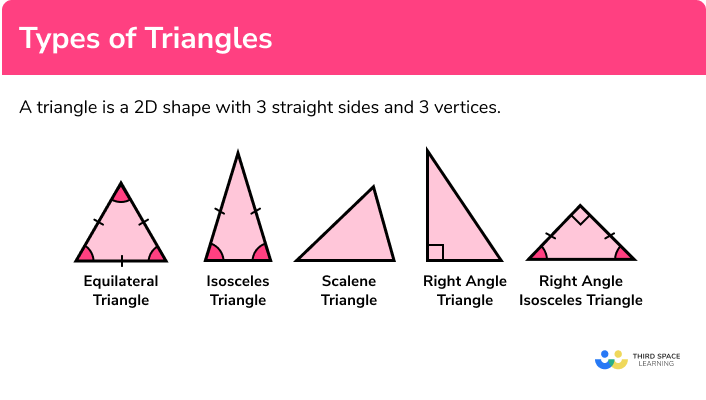
Types of triangles

There are 555 different types of triangle. Below is a table that describes the properties of each triangle.

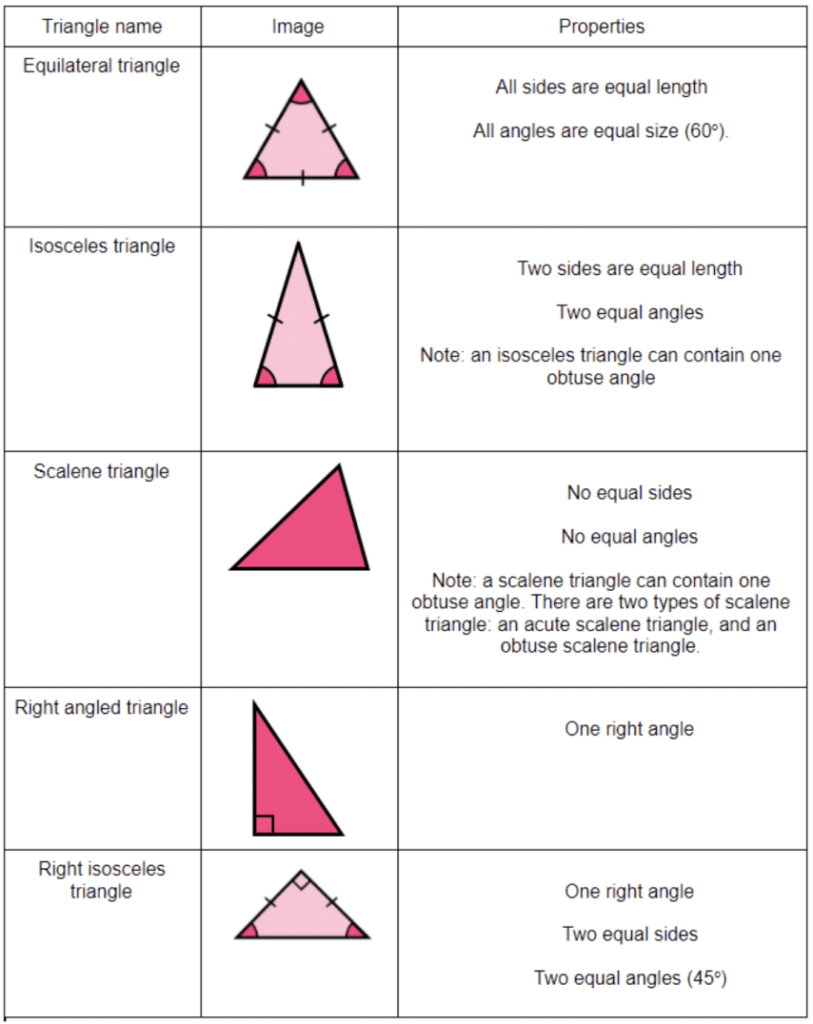
Properties of triangles are very important within geometry. They are one of the most common shapes to recognise for angles in parallel lines, circle theorems, interior angles, trigonometry, Pythagoras’ theorem, and many more. You therefore must be familiar with their individual properties.

Triangle properties

We need to know the types of triangles and their properties. We know that all triangles have 3 sides and 3 angles. We also need to recognise that there are lots of different types of triangles and they are all unique because of the collection of properties each shape may have. 

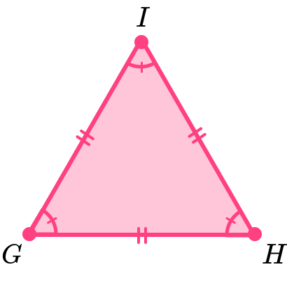
We can recognise equilateral triangles because they have 3 equal sides and 3 equal angles. Equal sides are often labelled with dashes. 

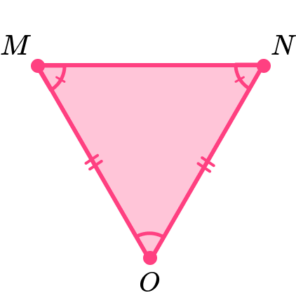
We can recognise isosceles triangles because they have 2 equal sides and 2 equal angles. The 2 equal angles are the base angles of the isosceles triangle. 

We can recognise scalene triangles because all the sides are different and all the angles are different. 

We can recognise right angled triangles because they have one right angle. 

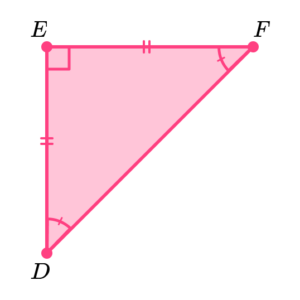
We can recognise right angled isosceles triangles because they have 1 right angle, 2 equal sides and 2 equal angles. 

We can use these properties to solve problems and find missing angles. 

Is this statement true or false?

An equilateral triangle has three equal sized side lengths and two equal sized angles.

Answer: False

Equilateral triangles have 3 equal sides and 3 equal angles. 

Find the missing angle.
 

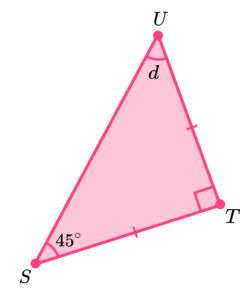
Answer:

This is a right angled isosceles triangle because it has 1 right angle and 2 equal sides marked with a dash.

So, Angle d=45°d=45°d=45°.

Angles in a triangle

Triangles can contain acute angles, a right angle, or one obtuse angle.
A triangle cannot contain more than one right angle, obtuse angle, or a reflex angle. The only two types of triangles that can contain an obtuse angle are an isosceles triangle and a scalene triangle. 

Here are two examples of these obtuse triangles:

The sum of angles in a triangle is 180°180°180°.

This property helps to find angles in any polygon as a polygon can be triangulated (split into triangles) and therefore the interior angles can be calculated. 

How to classify a triangle

In order to classify a triangle:

1. Determine the size of the angles/side lengths within the triangle.

2. Recognise the other properties of the triangle.